第一章 单元测试
1、判断题:
方阵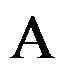 可逆是
可逆是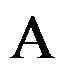 无0为其特征值的必要但不充分条件。 ( )
无0为其特征值的必要但不充分条件。 ( )
选项:
A:错
B:对
答案: 【错】
2、多选题:
相似矩阵有相同的 ( )。
选项:
A:特征向量
B:行列式
C:迹
D:特征值
答案: 【行列式;
迹;
特征值】
3、单选题:
矩阵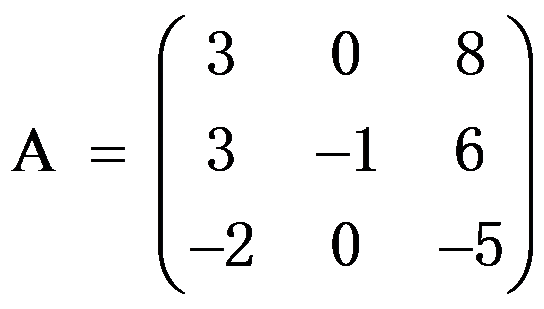 的初等因子为 ( )。
的初等因子为 ( )。
选项:
A: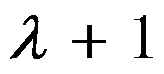
B: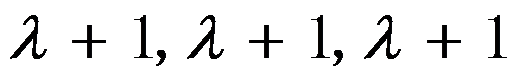
C: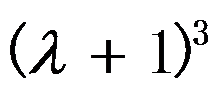
D: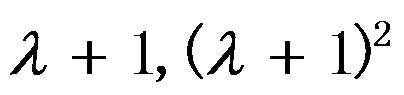
答案: 【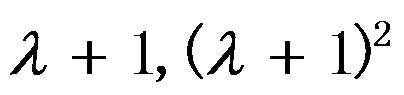
】
4、判断题:
方阵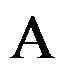 的每个特征值都是
的每个特征值都是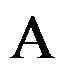 的最小多项式的根。 ( )
的最小多项式的根。 ( )
选项:
A:错
B:对
答案: 【对】
5、判断题:
酉矩阵的行列式为1。 ( )
选项:
A:错
B:对
答案: 【错】
第二章 单元测试
1、单选题:
矩阵范数和谱半径之间有什么关系?( )
选项:
A:矩阵范数大于或者等于谱半径
B:矩阵范数小于或者等于谱半径
C:两者相等
D:两者之间没有任何关系
答案: 【矩阵范数大于或者等于谱半径】
2、单选题:
矩阵的1范数,2范数以及∞范数之间有何关系?( )
选项:
A:矩阵的1范数一定大于其∞范数
B:矩阵的1范数一定大于其2范数
C:它们之间没有一定的关系
D:矩阵的∞范数一定大于其1范数
答案: 【它们之间没有一定的关系】
3、单选题:
如何计算矩阵的条件数?( )
选项:
A:矩阵范数的平方
B:矩阵的范数乘以其逆矩阵的范数
C:矩阵的范数乘以其范数的逆
D:逆矩阵范数的平方
答案: 【矩阵的范数乘以其逆矩阵的范数】
4、判断题:
矩阵范数与向量范数一定是相容的?( )
选项:
A:对
B:错
答案: 【错】
5、单选题:
矩阵范数所满足的性质比向量范数满足的性质多了哪一条?( )
选项:
A:三角不等式
B:齐次性
C:非负性
D:相容性
答案: 【相容性】
第三章 单元测试
1、单选题:
对矩阵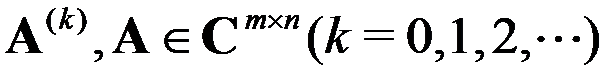 ,若任意一种矩阵范数
,若任意一种矩阵范数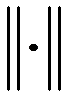 均满足
均满足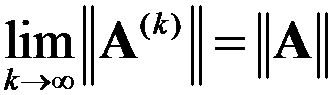 ,则
,则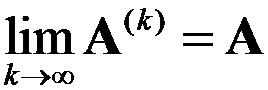 .( )
.( )
选项:
A:无法判断.
B:不成立;
C:不一定成立;
D:一定成立;
答案: 【
2、判断题:
试分析:对矩阵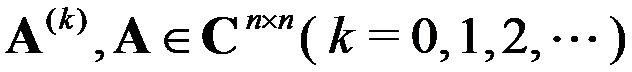 ,
,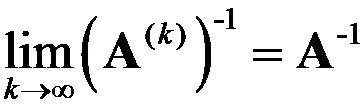 . ( )
. ( )
选项:
A:错
B:对
答案: 【】
3、判断题:
对矩阵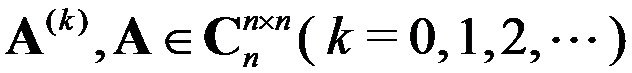 ,
,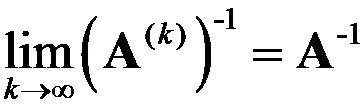 . ( )
. ( )
选项:
A:对
B:错
答案: 【】
4、判断题:
绝对收敛的矩阵级数一定收敛. ( )
选项:
A:对
B:错
答案: 【】
5、单选题:
对矩阵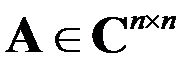 ,若矩阵
,若矩阵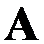 的某一种矩阵范数
的某一种矩阵范数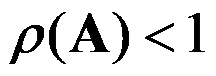 ,则幂级数
,则幂级数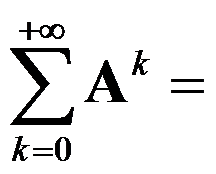 ( ).
( ).
选项:
A: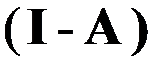 ;
;
B: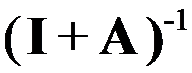 .
.
C: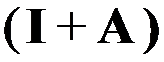 ;
;
D: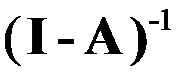 ;
;
答案: 【】
第四章 单元测试
1、判断题:
设矩阵 是Hermite正定矩阵,则在保证分解矩阵
是Hermite正定矩阵,则在保证分解矩阵 主对角元素全为正的情况下,矩阵
主对角元素全为正的情况下,矩阵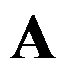 存在唯一的Cholesky分解
存在唯一的Cholesky分解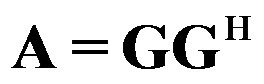 。( )
。( )
选项:
A:对
B:错
答案: 【】
2、判断题:
设矩阵 ,则矩阵
,则矩阵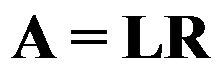 ,若矩阵
,若矩阵 为单位下三角矩阵,
为单位下三角矩阵,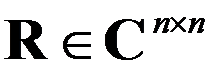 为上三角矩阵,则该分解称为Crout分解。( )
为上三角矩阵,则该分解称为Crout分解。( )
选项:
A:对
B:错
答案: 【】
3、判断题:
设矩阵 ,则
,则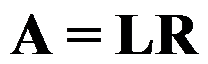 ,其中
,其中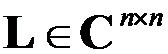 为单位下三角矩阵,
为单位下三角矩阵, 为上三角矩阵,为矩阵
为上三角矩阵,为矩阵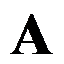 的Doolittle分解。( )
的Doolittle分解。( )
选项:
A:对
B:错
答案: 【】
4、判断题:
Householder矩阵是酉矩阵。( )
选项:
A:错
B:对
答案: 【】
5、判断题:
Givens矩阵是Hermite矩阵。( )
选项:
A:对
B:错
答案: 【】
第五章 单元测试
1、判断题:
1 设矩阵 ,且
,且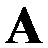 的
的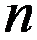 个盖尔圆都是孤立的,则矩阵
个盖尔圆都是孤立的,则矩阵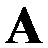 有
有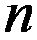 个互不相同的是特征值.( )
个互不相同的是特征值.( )
选项:
A:错
B:对
答案: 【】
2、多选题:
2 设矩阵 ,矩阵
,矩阵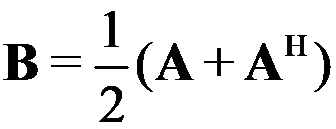 ,矩阵
,矩阵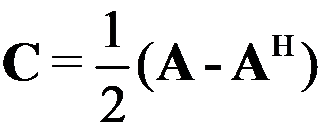 ,
,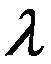 是矩阵
是矩阵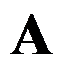 的任意特征值,则下列说法正确的是( ).
的任意特征值,则下列说法正确的是( ).
选项:
A: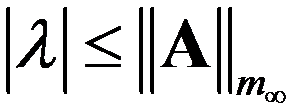
B: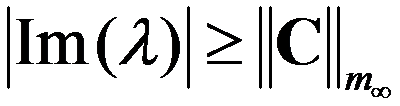
C: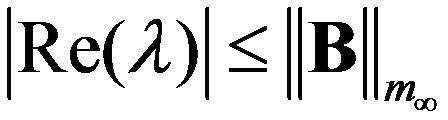
D: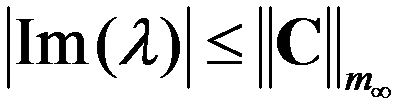
答案: 【】
3、判断题:
3 设矩阵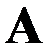 是
是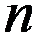 阶酉矩阵,
阶酉矩阵,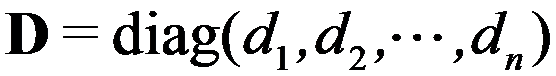 ,则
,则 的特征值
的特征值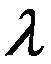 满足
满足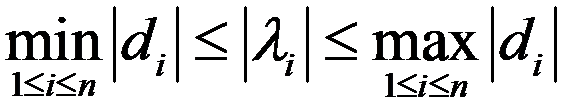 ( ).
( ).
选项:
A:对
B:错
答案: 【】
4、判断题:
任何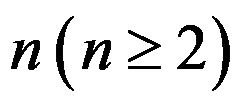 阶矩阵的盖尔圆都可以通过相似变换隔离成
阶矩阵的盖尔圆都可以通过相似变换隔离成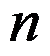 个孤立的盖尔圆。( )
个孤立的盖尔圆。( )
选项:
A:错
B:对
答案: 【】
5、判断题:
设矩阵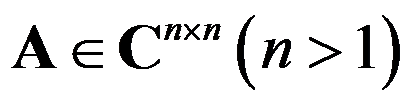 有
有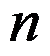 个孤立的盖尔圆,且原点
个孤立的盖尔圆,且原点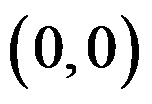 不在这些盖尔圆中,则
不在这些盖尔圆中,则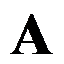 非奇异。( )
非奇异。( )
选项:
A:对
B:错
答案: 【】


评论0