第一章 单元测试
1、单选题:
已知等式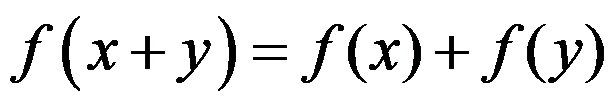 对全体实数成立,则
对全体实数成立,则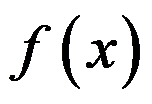 是 ( )
是 ( )
选项:
A:非奇非偶函数
B:既是奇函数又是偶函数
C:奇函数
D:偶函数
答案: 【奇函数】
2、单选题:
下列函数在给定区间内无界的是 ( )
选项:
A:
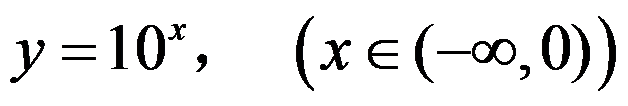
B:
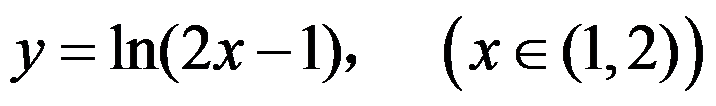
C:
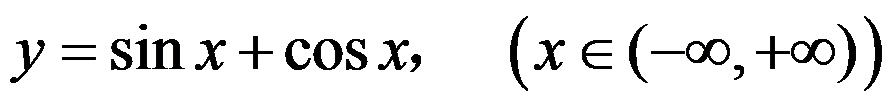
D:
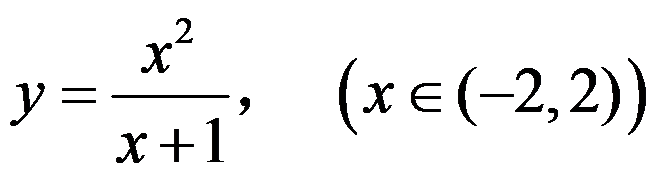
答案: 【
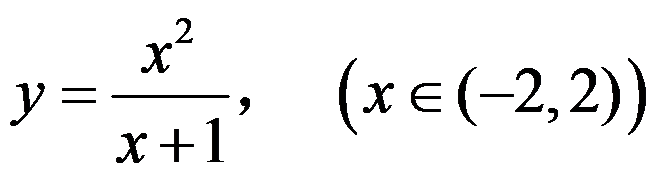
】
3、单选题:
已知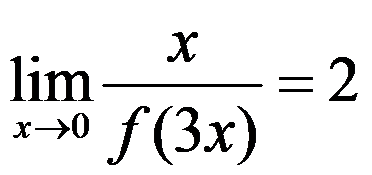 ,则
,则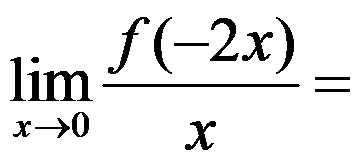 ( )
( )
选项:
A: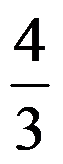
B: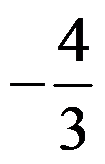
C: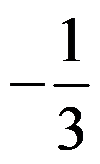
D: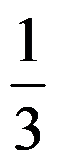
答案: 【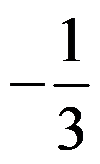
】
4、单选题:
设当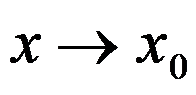 时,
时,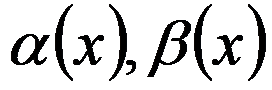 都是无穷小
都是无穷小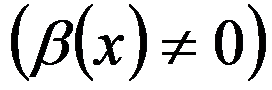 ,则当
,则当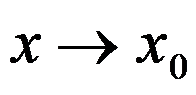 时,下列表达式中不一定为无穷小的是( )
时,下列表达式中不一定为无穷小的是( )
选项:
A: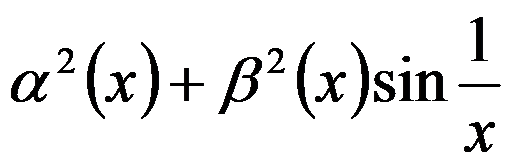
B: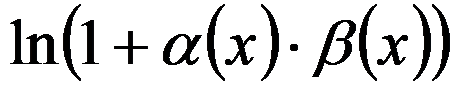
C: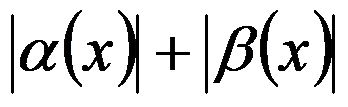
D: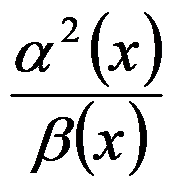
答案: 【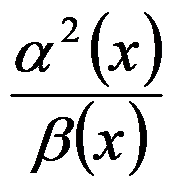
】
5、单选题:
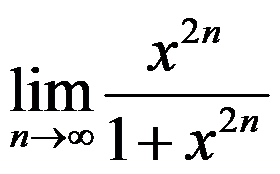 等于 ( )
等于 ( )
选项:
A: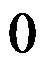
B:其他三个答案都不对
C:1
D: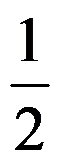
答案: 【其他三个答案都不对】
第二章 单元测试
1、单选题:
设函数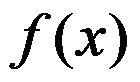 是可导函数,且
是可导函数,且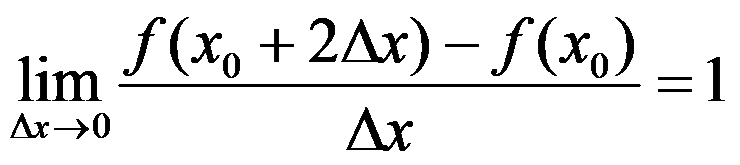 ,则
,则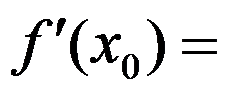 ( )
( )
选项:
A:0.5
B:
C:
D:
答案: 【0.5】
2、单选题:
设函数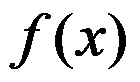 在
在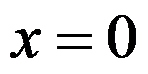 处连续,且
处连续,且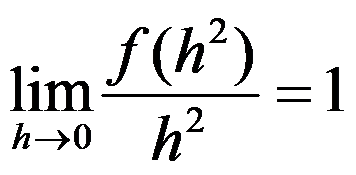 ,则( )
,则( )
选项:
A: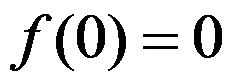 且
且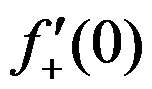 存在
存在
B: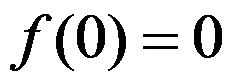 且
且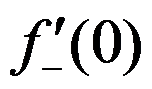 存在
存在
C: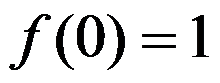 且
且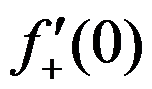 存在
存在
D: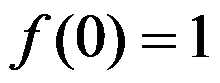 且
且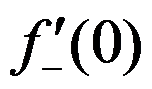 存在
存在
答案: 【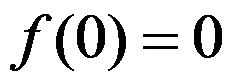 且
且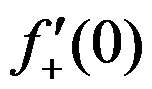 存在
存在
】
3、单选题:
设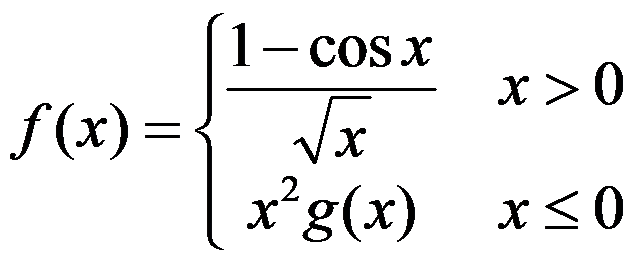 ,
,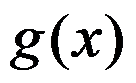 在
在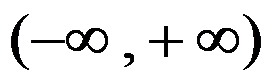 内有界,则
内有界,则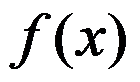 在
在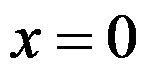 处( )
处( )
选项:
A:连续但不可导
B:极限存在但不连续
C:可导
D:极限不存在
答案: 【可导】
4、单选题:
设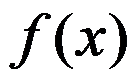 为奇函数,则其导数
为奇函数,则其导数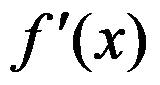 的奇偶性为( )
的奇偶性为( )
选项:
A:奇偶性不定
B:偶函数
C:非奇非偶
D:奇函数
答案: 【偶函数】
5、单选题:
下列命题中,与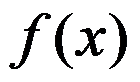 在
在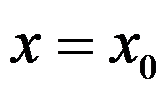 是否有定义无关的命题是( )
是否有定义无关的命题是( )
选项:
A: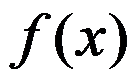 在
在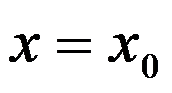 连续
连续
B: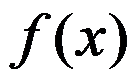 在
在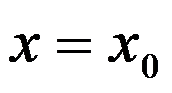 极限存在
极限存在
C: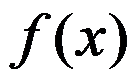 在
在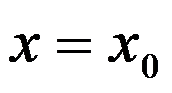 可微
可微
D: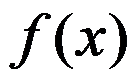 在
在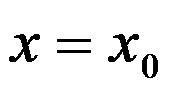 可导
可导
答案: 【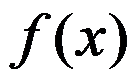 在
在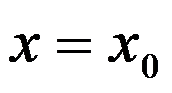 极限存在
极限存在
】
第三章 单元测试
1、单选题:
下列函数在给定区间上满足罗尔定理的有( ).
选项:
A: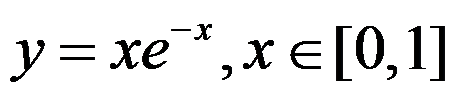
B: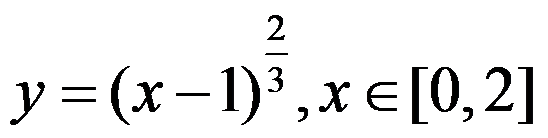
C: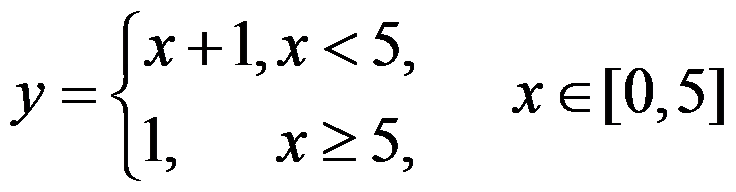
D: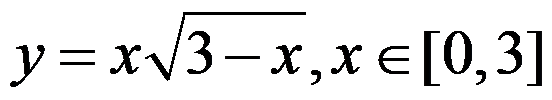
答案: 【
】
2、单选题:
下列函数在给定区间上满足拉格朗日定理的有( ).
选项:
A: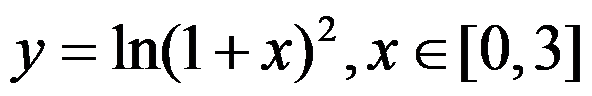
B: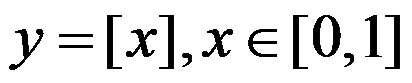
C: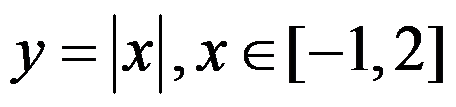
D: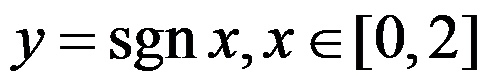
答案: 【
】
3、单选题:
下列函数在给定区间上不满足拉格朗日中值定理的有( )
选项:
A:
B: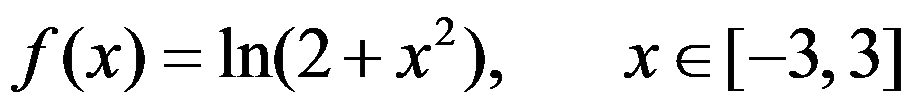
C: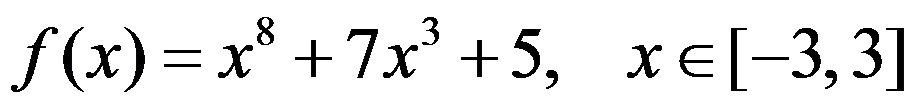
D: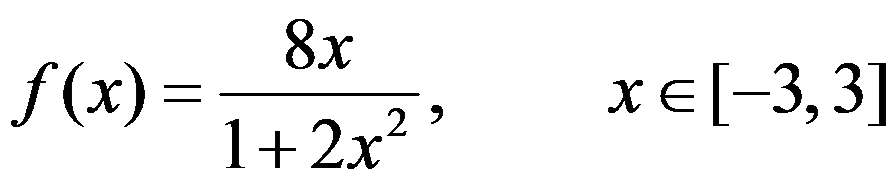
答案: 【
】
4、单选题:
若函数在区间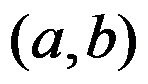 内可导,且
内可导,且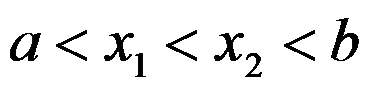 ,则至少存在一点
,则至少存在一点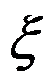 ,使得( )成立.
,使得( )成立.
选项:
A: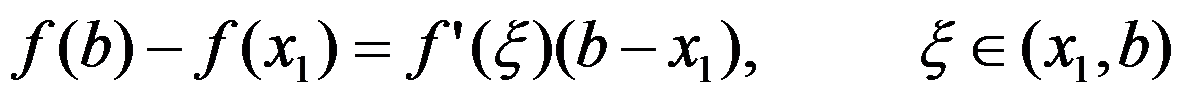
B: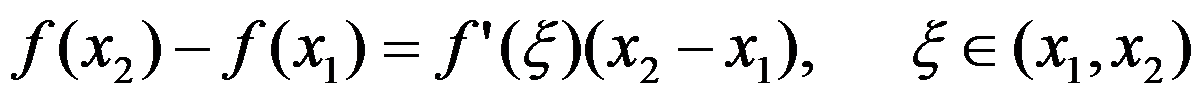
C: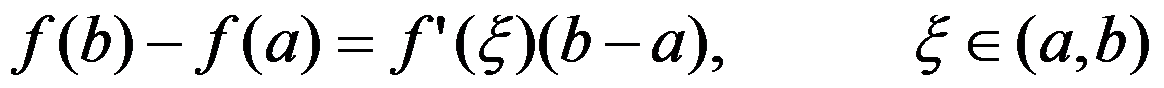
D: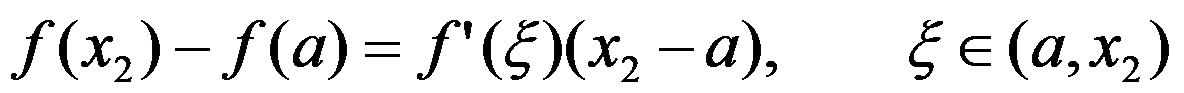
答案: 【
】
5、单选题:
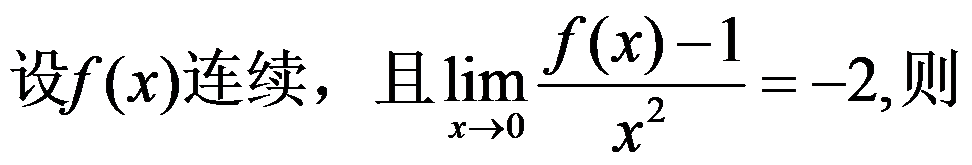 ( ).
( ).
选项:
A:
B: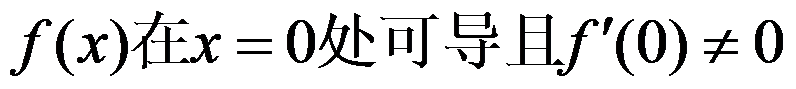
C: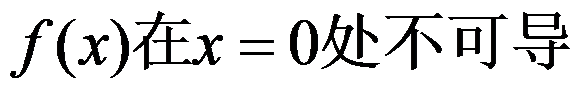
D:
答案: 【
】
第四章 单元测试
1、单选题:
若函数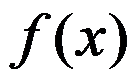 的一个原函数为
的一个原函数为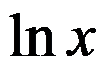 ,则一阶导数
,则一阶导数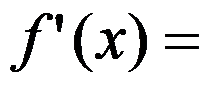 ( ).
( ).
选项:
A: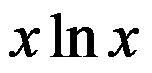
B: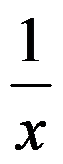
C: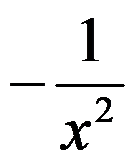
D: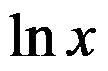
答案:
】
2、单选题:
已知函数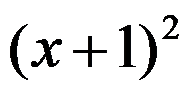 为
为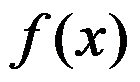 的一个原函数,则下列函数中( )为
的一个原函数,则下列函数中( )为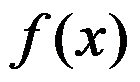 的原函数.
的原函数.
选项:
A: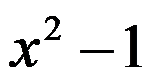
B: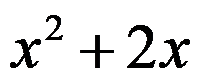
C: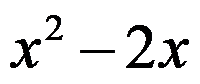
D: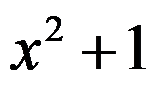
答案: 【
】
3、单选题:
若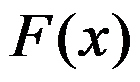 可导,且
可导,且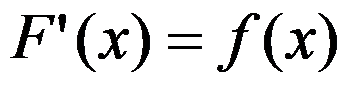 ,则不定积分
,则不定积分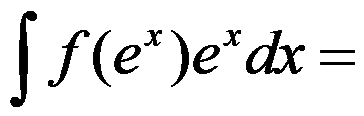 ( ).
( ).
选项:
A: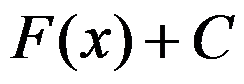
B: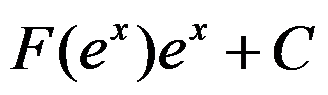
C: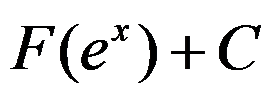
D: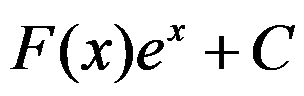
答案: 【
】
4、单选题:
若函数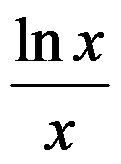 为
为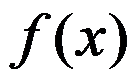 的一个原函数,则不定积分
的一个原函数,则不定积分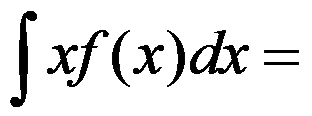 ( ).
( ).
选项:
A: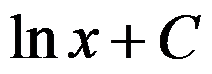
B: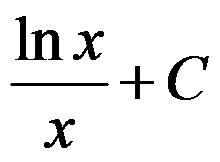
C: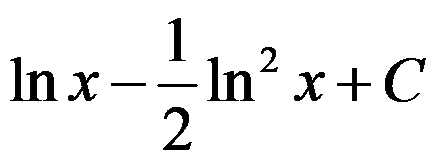
D: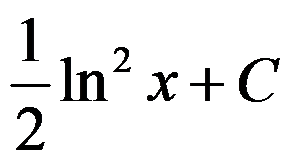
答案: 【
】
5、单选题:
若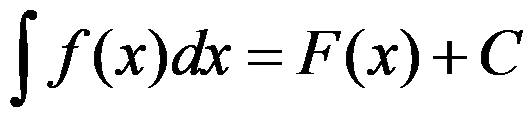 ,则
,则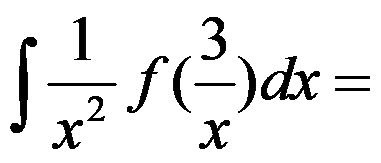 ( ).
( ).
选项:
A: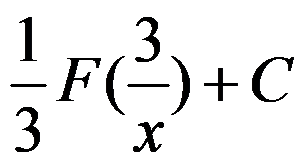
B: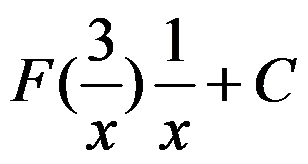
C: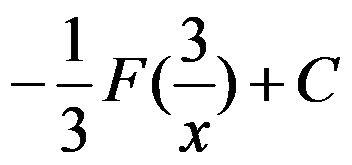
D: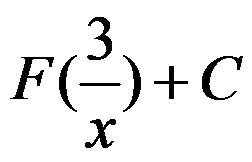
答案: 【
】
第五章 单元测试
1、单选题:
设积分区域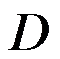 是由直线
是由直线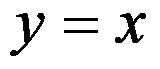 ,
,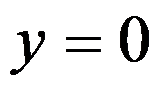 ,
,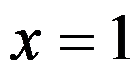 围成,则
围成,则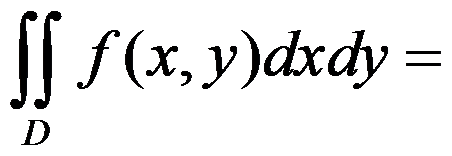 ( )
( )
选项:
A: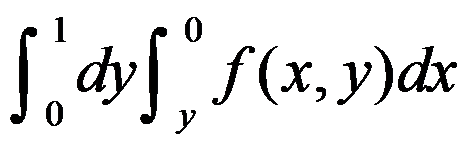
B: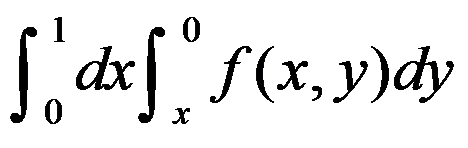
C: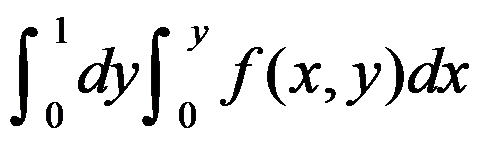
D: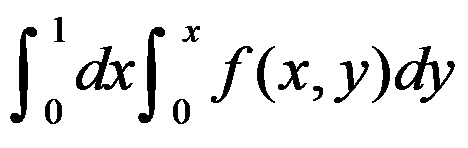
答案: 【
】
2、单选题:
设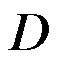 是方形域:
是方形域: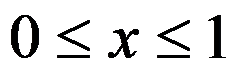 ,
,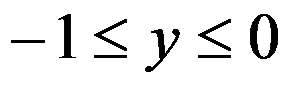 ,
,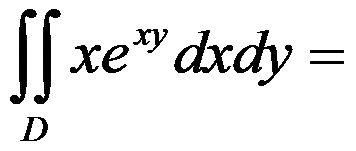 ( )
( )
选项:
A: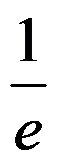
B:
C:
D: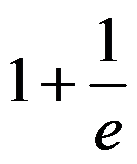
答案: 【
】
3、单选题:
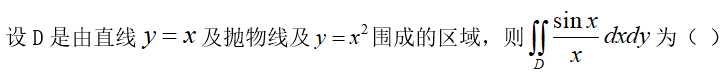
选项:
A: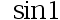
B:
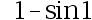
C: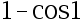
D: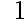
答案: 【
】
4、单选题:
设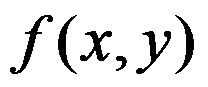 连续,且
连续,且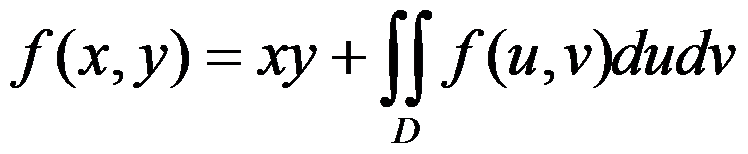 ,其中
,其中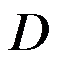 是由
是由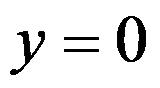 ,
,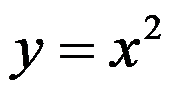 ,
,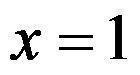 所围区域,则
所围区域,则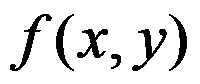 =( )
=( )
选项:
A:
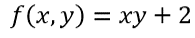
B:
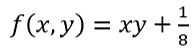
C:
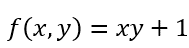
D:
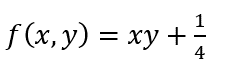
答案: 【
】
5、单选题:

选项:
A:
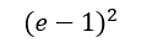
B:

C:
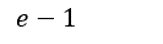
D:
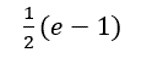
答案: 【
】
第六章 单元测试
1、单选题:
幂级数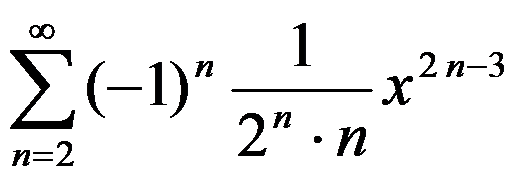 的收敛半径是( )
的收敛半径是( )
选项:
A: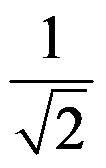
B:
C:
D: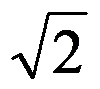
答案: 【
】
2、单选题:
级数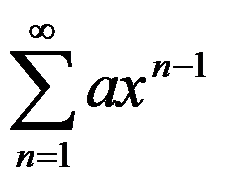 (
(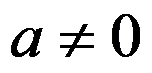 )收敛的条件是
)收敛的条件是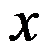 属于( )
属于( )
选项:
A: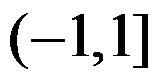
B: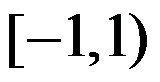
C: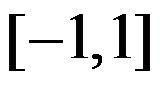
D: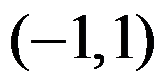
答案: 【
】
3、单选题:
幂级数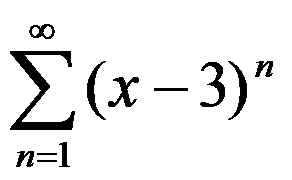 的收敛区间是( )
的收敛区间是( )
选项:
A: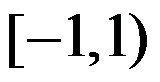
B: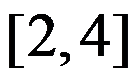
C: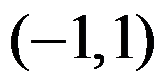
D: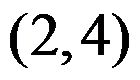
答案: 【
】
4、单选题:
幂级数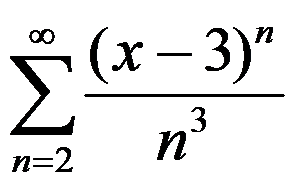 的收敛域是( )
的收敛域是( )
选项:
A: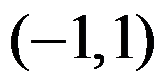
B: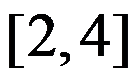
C: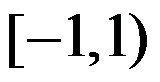
D: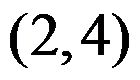
答案: 【
】
5、单选题:
幂级数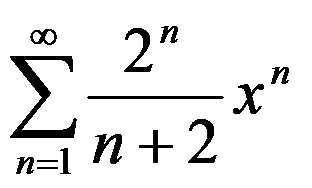 的收敛半径
的收敛半径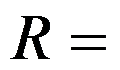 ( )
( )
选项:
A: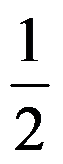
B:
C: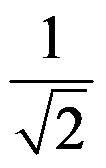
D:
答案: 【
】
第七章 单元测试
1、单选题:
已知微分方程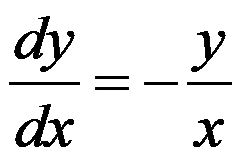 ,且
,且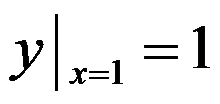 ,则其特解为( )
,则其特解为( )
选项:
A: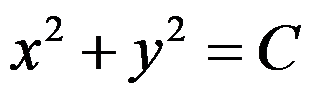 ,
, 是任意常数
是任意常数
B: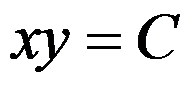 ,
, 是任意常数
是任意常数
C: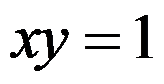
D: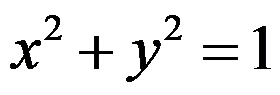
答案: 【
】
2、单选题:
已知微分方程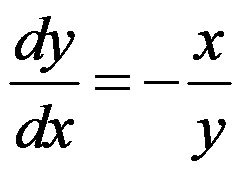 ,且
,且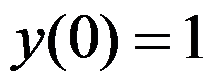 ,则其特解为( )
,则其特解为( )
选项:
A: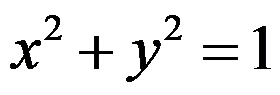
B: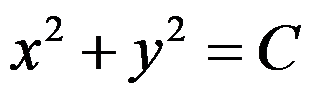 ,
, 是任意常数
是任意常数
C: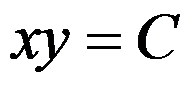 ,
, 是任意常数
是任意常数
D: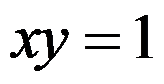
答案:
】
3、单选题:
已知微分方程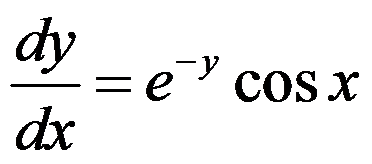 ,且
,且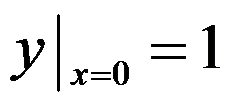 ,则其特解为( )
,则其特解为( )
选项:
A: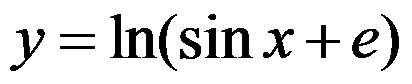
B: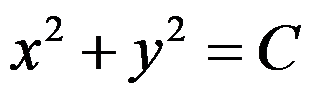 ,
, 是任意常数
是任意常数
C: ,
, 是任意常数
是任意常数
D: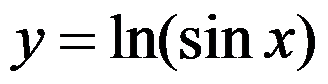
答案: 【
】
4、单选题:
已知微分方程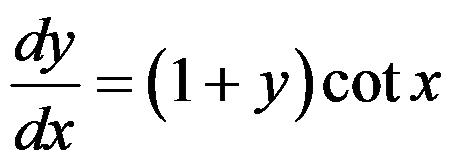 ,则其通解为( )
,则其通解为( )
选项:
A: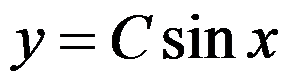
B: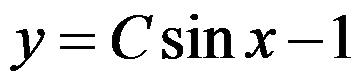 ,
, 是任意常数
是任意常数
C: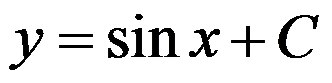 ,
, 是任意常数
是任意常数
D: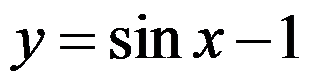
答案: 【
】
5、单选题:
已知微分方程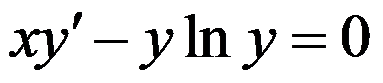 ,则其通解为( )
,则其通解为( )
选项:
A: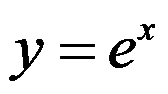
B: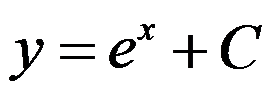 ,
, 是任意常数
是任意常数
C: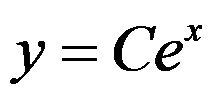 ,
, 是任意常数
是任意常数
D: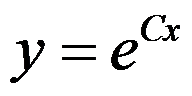 ,
, 是任意常数
是任意常数
答案: 【
】


评论0