第一章 单元测试
1、单选题:
设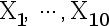 来自正态分布
来自正态分布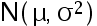 的样本,
的样本,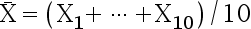 ,若
,若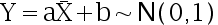 ,则 ( )
,则 ( )
选项:
A: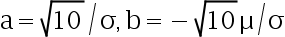
B: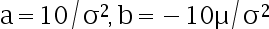
C: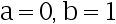
D: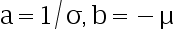
答案: 【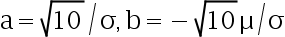
】
2、单选题:
设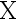 为一随机变量,其期望为
为一随机变量,其期望为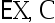 为任意常数,则( )
为任意常数,则( )
选项:
A: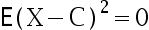
B: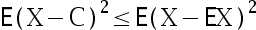
C: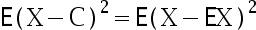
D: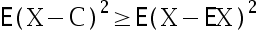
答案: 【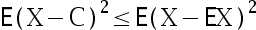
】
3、单选题:
设总体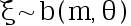 ,
,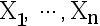 来自该总体的简单随机样本,
来自该总体的简单随机样本,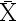 为样本均值,则
为样本均值,则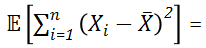 ( )
( )
选项:
A: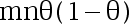
B: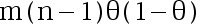
C: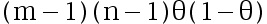
D: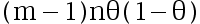
答案: 【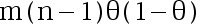
】
4、单选题:
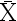 和
和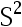 分别为样本均值和样本方差。记统计量
分别为样本均值和样本方差。记统计量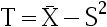 ,则
,则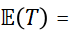 ( )
( )
选项:
A: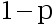
B: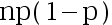
C: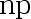
D: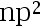
答案: 【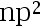
】
5、单选题:
设 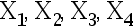 为来自正态总体
为来自正态总体 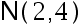 的简单随机样本, 则
的简单随机样本, 则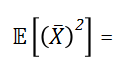 ( )
( )
选项:
A: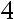
B: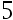
C: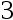
D: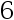
答案: 【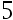
】
6、判断题:
设 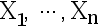 是来自泊松分布
是来自泊松分布 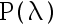 的样本, 则
的样本, 则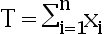 是充分统计量。( )
是充分统计量。( )
选项:
A:对
B:错
答案: 【对】
7、单选题:
设随机变量 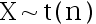 ,
, 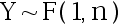 ,给定
,给定 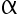 ,其中
,其中 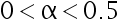 , 常数
, 常数 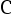 满足
满足 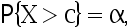 则
则 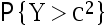 =( )
=( )
选项:
A: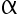
B: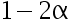
C: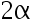
D: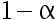
答案: 【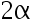
】
8、多选题:
设 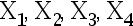 是来自正态总体
是来自正态总体 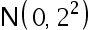 的简单随机 样本, 且
的简单随机 样本, 且 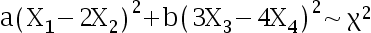 分布,则( )
分布,则( )
选项:
A: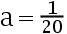
B: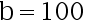
C: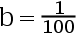
D: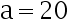
答案: 【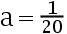
;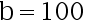
】
9、判断题:
设 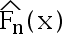 是总体
是总体 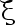 的经验分布函数, 而
的经验分布函数, 而 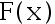 是总体
是总体 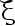 的分 布函教,在下列命题中, 对于每个给定的 x,
的分 布函教,在下列命题中, 对于每个给定的 x, 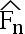 (x)满足依概率收敛于
(x)满足依概率收敛于 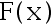 。( )
。( )
选项:
A:对
B:错
答案: 【对】
10、判断题:
设总体 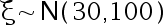 , 从总体
, 从总体 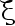 中抽取一个容量为 100 的 样本, 则
中抽取一个容量为 100 的 样本, 则 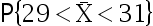 为0.626。( )
为0.626。( )
选项:
A:错
B:对
答案: 【对】
第二章 单元测试
1、判断题:
设 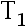 与
与 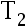 分别是
分别是 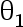 与
与 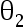 的 UMVUE, 则对任意的非零常数
的 UMVUE, 则对任意的非零常数 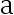 与
与 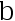 ,
,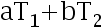 是
是 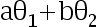 的 UMVUE( )
的 UMVUE( )
选项:
A:对
B:错
答案: 【对】
2、判断题:
设 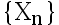 为一维随机变量序列,满足
为一维随机变量序列,满足 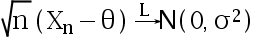 , 则 对于给定的函数
, 则 对于给定的函数 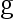 及一个指定的值
及一个指定的值 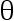 , 使得
, 使得 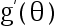 存在, 且不为 0 , 则在一维情形下
存在, 且不为 0 , 则在一维情形下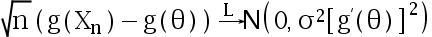 成立( )
成立( )
选项:
A:错
B:对
答案: 【对】
3、单选题:
随机地取 8 只活塞环,测得它们的直径为(单位: 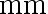 ) 74.001,74.005,74.003,74.001,74.000,73.993,74.006,74.002。 试求总体均值
) 74.001,74.005,74.003,74.001,74.000,73.993,74.006,74.002。 试求总体均值 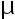 及方差
及方差 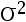 的矩估计值为( )
的矩估计值为( )
选项:
A: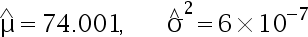
B: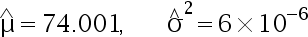
C: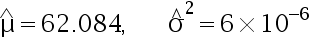
D: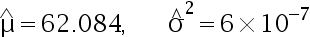
答案: 【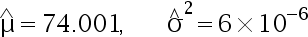
】
4、单选题:
设总体 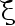 的概率密度为
的概率密度为
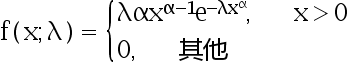
其中 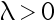 是未知参数,
是未知参数, 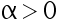 是已知常数,根据来自总体
是已知常数,根据来自总体 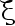 的简单随机样本
的简单随机样本 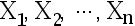 , 求
, 求 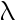 的最大似然估计量
的最大似然估计量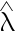 ( )
( )
选项:
A: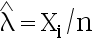
B: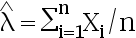
C: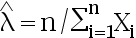
D: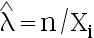
答案: 【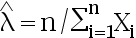
】
5、单选题:
设总体 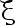 在
在 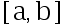 上服从均匀分布,
上服从均匀分布, 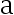 、
、 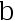 未知
未知 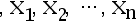 是样本值,则
是样本值,则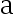 、
、 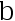 的极大似然估计量为( )
的极大似然估计量为( )
选项:
A: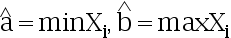
B: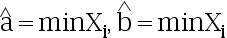
C: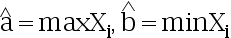
D: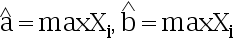
答案: 【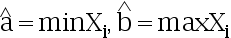
】
6、判断题:
若 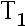 与
与 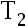 是未知参数
是未知参数 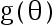 的两个 UMVUE, 则
的两个 UMVUE, 则 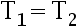 依概率几乎处处成立,这个命题表明:
依概率几乎处处成立,这个命题表明: 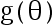 的UMVUE在几乎处处的意义下是唯一的。( )
的UMVUE在几乎处处的意义下是唯一的。( )
选项:
A:错
B:对
答案: 【对】
7、单选题:
设 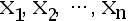 是来自指数分布
是来自指数分布 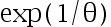 的一个样本值,求
的一个样本值,求 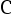 使
使 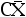 在均方误差准 则下是
在均方误差准 则下是 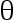 的最优估计。( )
的最优估计。( )
选项:
A: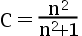
B: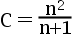
C: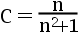
D: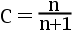
答案: 【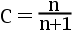
】
8、判断题:
设某团体人的高度 (单位:厘米)服从均值为 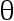 、标准差为 5 的正态分布。又设
、标准差为 5 的正态分布。又设 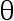 的 先验分布为
的 先验分布为 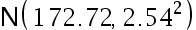 , 如今对随机选出的 10 个人测量高度,其平均高度为
, 如今对随机选出的 10 个人测量高度,其平均高度为 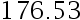 厘米, 求
厘米, 求 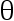 的后验分布为
的后验分布为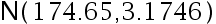 ( )
( )
选项:
A:错
B:对
答案: 【对】
9、判断题:
考察均匀分布族 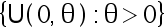 , 则不管样本容量
, 则不管样本容量 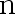 为多大,
为多大, 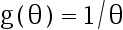 不是可估 参数。( )
不是可估 参数。( )
选项:
A:错
B:对
答案: 【对】
10、判断题:
设 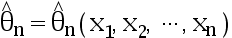 是
是 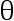 的一个估计,若
的一个估计,若 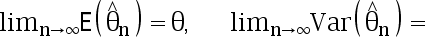 0 ,则
0 ,则 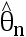 不是
不是 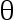 的相合估计( )
的相合估计( )
选项:
A:错
B:对
答案: 【错】
第三章 单元测试
1、单选题:
设总体分布为 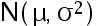 , 其中
, 其中 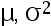 未知,
未知, 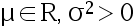 。 指出下列的统计量假设中, 哪个是复合假设( )
。 指出下列的统计量假设中, 哪个是复合假设( )
选项:
A: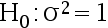
B: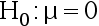
C: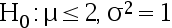
D: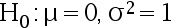
答案: 【
】
2、多选题:
设 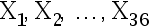 是取自正态总体
是取自正态总体 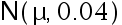 的简单随机样 本, 检验问题
的简单随机样 本, 检验问题
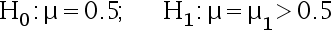
检验的显著性水平 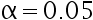 , 取拒绝域为
, 取拒绝域为 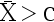 , 则
, 则 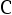 为多少?若
为多少?若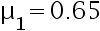 ,则犯第二类错误的概率
,则犯第二类错误的概率 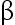 为多少( )
为多少( )
选项:
A: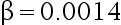
B: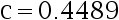
C: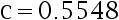
D: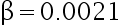
答案: 【
】
3、单选题:
设总体 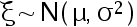 ,
, 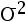 已知,
已知, 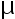 未知,
未知, 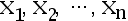 是来 自总体
是来 自总体 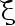 的样本观察值,已知
的样本观察值,已知 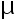 的置信水平为
的置信水平为 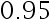 的置信区间为
的置信区间为 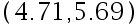 , 则取 显著性水平
, 则取 显著性水平 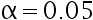 时, 检验假设
时, 检验假设 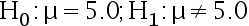 的结果是( )
的结果是( )
选项:
A:条件不足无法检验
B:拒绝 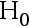
C:接受 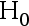
D:不能确定
答案: 【
】
4、判断题:
设 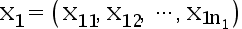 是来自正态总体
是来自正态总体 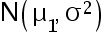 的一个样本值,
的一个样本值,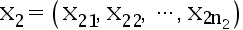 是来自另一个正态总体
是来自另一个正态总体 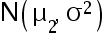 的一个样本值,两个样本独立,两方差相等但未知, 对如下一对假设
的一个样本值,两个样本独立,两方差相等但未知, 对如下一对假设 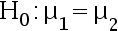 ;
;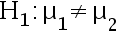 求广义似然比检验。具体如下:参数空间
求广义似然比检验。具体如下:参数空间  及其子集
及其子集 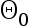 分别为
分别为

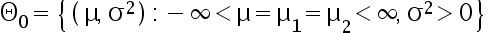
( )
选项:
A:错
B:对
答案: 【】
5、单选题:
设样本 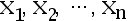 来自均匀分布
来自均匀分布 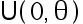 的样本值, 其中未知参数
的样本值, 其中未知参数 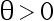 , 设
, 设 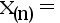
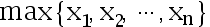 , 对检验问题
, 对检验问题 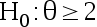 ;
;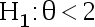 , 若取拒绝域为
, 若取拒绝域为 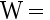
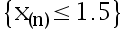 ,若要使犯第
,若要使犯第 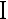 类错误的概率的最大值不超过
类错误的概率的最大值不超过 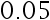 ,
, 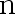 至少应取多大?( )
至少应取多大?( )
选项:
A:10
B:11
C:12
D:9
答案: 【】
6、判断题:
在假设检验中,若检验结果是接受原假设,检验可能犯第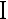 类错误。若检验结果 是拒绝原假设, 则又可能犯第 II 类错误。( )
类错误。若检验结果 是拒绝原假设, 则又可能犯第 II 类错误。( )
选项:
A:对
B:错
答案: 【】
7、单选题:
若设 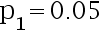 ,
, 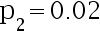 ,在犯第
,在犯第 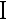 、
、 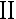 类错误的概率分别为
类错误的概率分别为 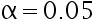 、
、 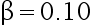 ,下为区分
,下为区分  与
与 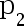 需要多大样本量( )
需要多大样本量( )
选项:
A: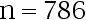
B: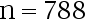
C: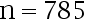
D: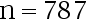
答案: 【
】
8、单选题:
设一个单一观测的样本 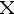 取自密度函数为
取自密度函数为 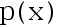 的总体,对
的总体,对  考虑统计假设:
考虑统计假设:
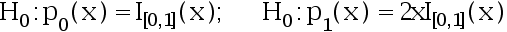
若其拒绝域的形式为 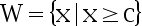 ,试确定一个
,试确定一个 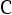 , 使得犯第一、 二类错误的概率满足
, 使得犯第一、 二类错误的概率满足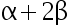 值取最小( )
值取最小( )
选项:
A: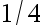
B: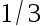
C: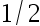
D: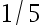
答案: 【
】
9、单选题:
考虑如下单边检验问题:

设基于样本 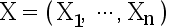 的分布为连续型指数分布族:
的分布为连续型指数分布族:
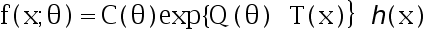
其中 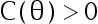 和
和 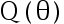 为
为 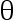 的函数,
的函数, 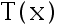 、
、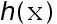 为样本
为样本 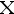 的函数。 若参数空间
的函数。 若参数空间  为
为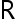 上的一有限或无限区间,
上的一有限或无限区间,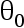 为
为  的一个内点且
的一个内点且 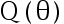 为
为 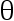 的严格减函数,则上述检验问题的水平为
的严格减函数,则上述检验问题的水平为 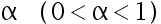 的UMP存在,其拒绝域的形式为( )。
的UMP存在,其拒绝域的形式为( )。
选项:
A: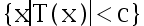
B: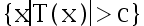
C: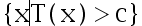
D: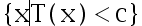
答案: 【
】
10、单选题:
设两独立总体 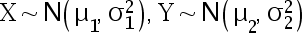 , 检验假设
, 检验假设 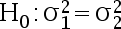 ;
;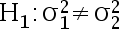 ,
,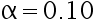 。 从
。 从 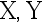 分别抽取容量为
分别抽取容量为 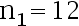 、
、 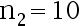 的样本,算得
的样本,算得 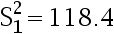 、
、 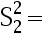
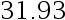 。 则正确的检验为( )
。 则正确的检验为( )
选项:
A:用 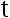 检验法,接受
检验法,接受 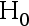
B:用 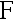 检验法, 拒绝
检验法, 拒绝 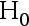
C:用 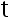 检验法,拒绝
检验法,拒绝 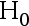
D:用 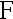 检验法,接受
检验法,接受 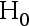
答案: 【
】
第四章 单元测试
1、单选题:
设大学生男生身高的总体 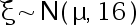 (单位:
(单位: 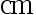 ), 若要使其平均身高置信水平为
), 若要使其平均身高置信水平为 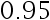 的置信区间长度小于 1.2 , 问至少应抽查多少名学生的身高( )
的置信区间长度小于 1.2 , 问至少应抽查多少名学生的身高( )
选项:
A:168
B:171
C:169
D:170
答案: 【】
2、单选题:
经验表明:棉纱的断裂负荷(单位是百分之一牛顿)服从正态分布。现从一批棉纱中随机抽取12段棉纱,测得其断裂负荷为
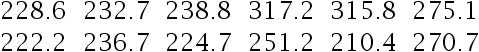
求棉纱断裂负荷的水平为 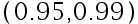 的容忍区间。( )
的容忍区间。( )
选项:
A: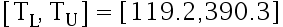
B: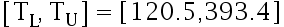
C: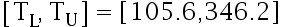
D: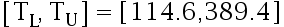
答案: 【
】
3、单选题:
设 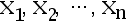 是来自正态总体
是来自正态总体 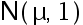 的一个样本值。 要使
的一个样本值。 要使 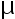 的区间估计
的区间估计 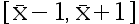 的置信系数为
的置信系数为 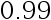 , 则至少需要多少样本量。( )
, 则至少需要多少样本量。( )
选项:
A:6
B:7
C:8
D:9
答案: 【】
4、单选题:
设 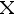 是从指数分布
是从指数分布 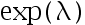 中随机抽得的单个观察值, 若取
中随机抽得的单个观察值, 若取 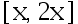 为
为 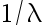 的区间估计,该区间的置信系数为多少( )
的区间估计,该区间的置信系数为多少( )
选项:
A:0.2387
B:0.1026
C:0.0717
D:0.2107
答案: 【】
5、单选题:
设一批零件的长度服从正态分布 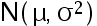 ,其中
,其中 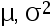 均未知,现从中随机抽取 16 个零件,测得样本均值
均未知,现从中随机抽取 16 个零件,测得样本均值 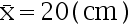 ,样本标准差
,样本标准差 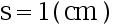 。 则
。 则 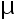 的置信度为
的置信度为 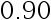 的置信区间是( )
的置信区间是( )
选项:
A:
B:
C:
D:
答案: 【
】
6、单选题:
设总体 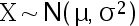 ,已知
,已知 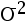 ,则样本容量
,则样本容量 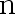 至少为多少时,才能保证
至少为多少时,才能保证 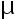 的置信度
的置信度 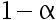 的置信区间长度不大于
的置信区间长度不大于 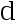 。( )
。( )
选项:
A: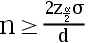
B: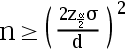
C: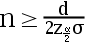
D: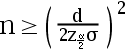
答案: 【
】
7、单选题:
设 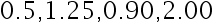 取自对数正态总体
取自对数正态总体 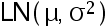 , 其密度为
, 其密度为
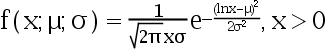
若设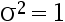 ,则
,则 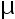 的
的 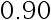 单侧置信上限为( )
单侧置信上限为( )
选项:
A:5.37245
B:4.89325
C:4.90789
D:5.89764
答案: 【
8、单选题:
用仪器测某物理量 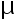 , 其测量值服从正态分布, 其标准差
, 其测量值服从正态分布, 其标准差 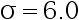 。现问至少要重 复测量多少次,才能使
。现问至少要重 复测量多少次,才能使 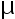 的
的 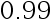 置信区间的长度为
置信区间的长度为 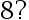 ( )
( )
选项:
A:13
B:15
C:16
D:14
答案: 【】
9、单选题:
初生婴儿的体重 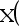 单位: 公斤
单位: 公斤 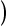 服从正态分布
服从正态分布 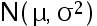 , 要使初生婴儿的平均重 量
, 要使初生婴儿的平均重 量 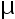 的
的 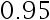 置信区间长度不超过
置信区间长度不超过 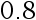 公斤, 至少应取多少样本量? 已知对近期出生的 4 个婴儿体重测得样本标准差
公斤, 至少应取多少样本量? 已知对近期出生的 4 个婴儿体重测得样本标准差 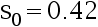 (公斤)。( )
(公斤)。( )
选项:
A:12
B:14
C:13
D:15
答案: 【】
10、单选题:
某种聚合物中的含氯量服从正态分布, 现已抽取 8 个样品, 测得样本标准差为0.84。为使平均含氯量的 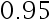 置信区间长度不超过 1 , 还需补抽多少个样品?( )
置信区间长度不超过 1 , 还需补抽多少个样品?( )
选项:
A:6
B:9
C:8
D:7
答案: 【】


评论0