第一章 单元测试
1、单选题:
下列对任意复数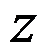 均成立的等式为( )。
均成立的等式为( )。
选项:
A:
B: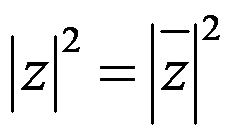
C: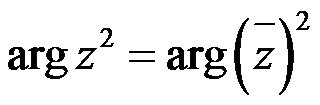
D:
答案: 【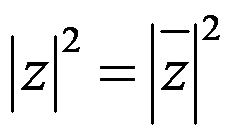
】
2、单选题:
下列说法中正确的是( )。
选项:
A: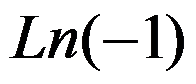 的实部等于0
的实部等于0
B: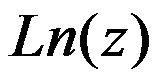 在
在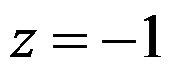 处无定义
处无定义
C: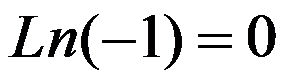
D: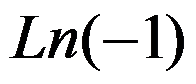 的虚部等于
的虚部等于
答案: 【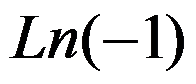 的实部等于0
的实部等于0
】
3、判断题:
该式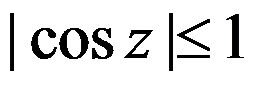 恒成立。( )
恒成立。( )
选项:
A:错
B:对
答案: 【错】
4、判断题:
该式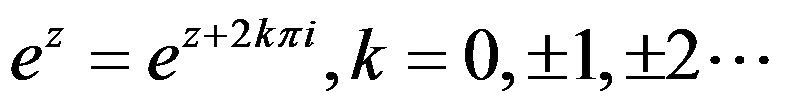 是恒成立的。( )
是恒成立的。( )
选项:
A:错
B:对
答案: 【对】
5、判断题:
设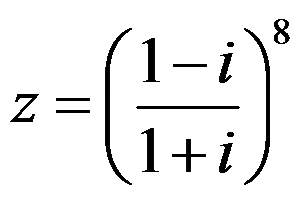 ,则
,则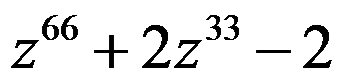 的值为1。( )
的值为1。( )
选项:
A:错
B:对
答案: 【对】
第二章 单元测试
1、单选题:
下例函数中为解析函数的为( )。
选项:
A: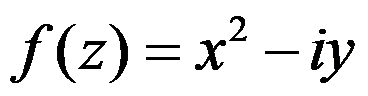
B: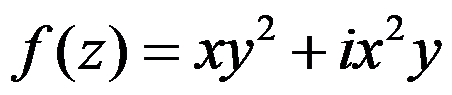
C: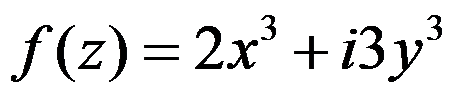
D: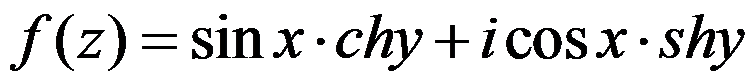
答案: 【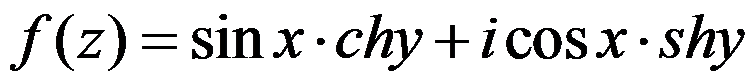
】
2、单选题:
函数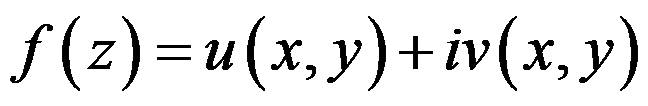 解析,则下列命题中错误的是( )。
解析,则下列命题中错误的是( )。
选项:
A: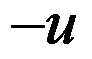 是
是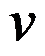 的共轭调和函数
的共轭调和函数
B: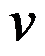 是
是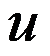 的共轭调和函数
的共轭调和函数
C: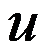 是
是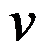 的共轭调和函数
的共轭调和函数
D: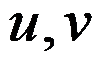 均是调和函数
均是调和函数
答案: 【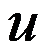 是
是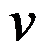 的共轭调和函数
的共轭调和函数
】
3、判断题:
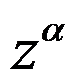 (
(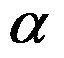 不等于整数)的每一个分支在除去原点的复平面上连续。( )
不等于整数)的每一个分支在除去原点的复平面上连续。( )
选项:
A:错
B:对
答案: 【错】
4、判断题:
解析函数的导函数仍为解析函数。( )
选项:
A:错
B:对
答案: 【对】
5、判断题:
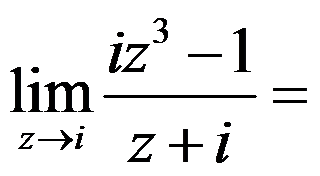 0。( )
0。( )
选项:
A:对
B:错
答案: 【对】
第三章 单元测试
1、单选题:
设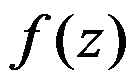 在单连通域
在单连通域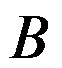 内解析,
内解析, 为
为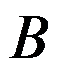 内任一闭曲线,则必有( )。
内任一闭曲线,则必有( )。
选项:
A: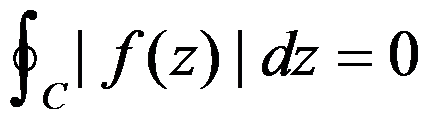
B: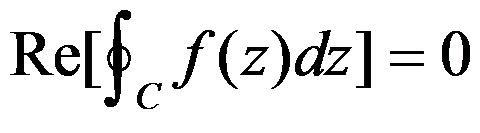
C: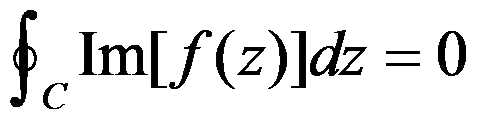
D:
答案: 【
】
2、单选题:
设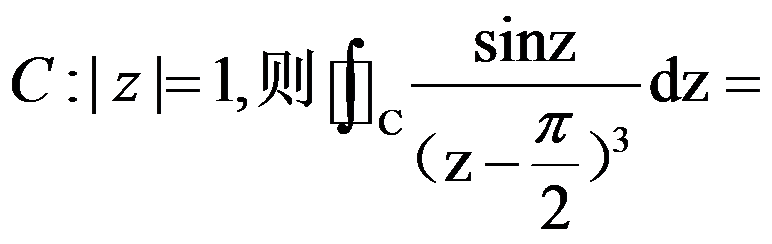 ( )。
( )。
选项:
A: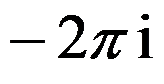
B:0
C: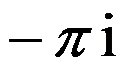
D: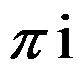
答案: 【】
3、判断题:
设 是一条简单正向闭曲线,
是一条简单正向闭曲线,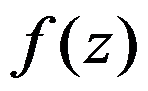 在以
在以 为边界的有界闭区域
为边界的有界闭区域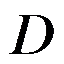 上解析,
上解析, 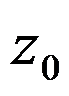 为
为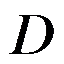 内任一点,那么
内任一点,那么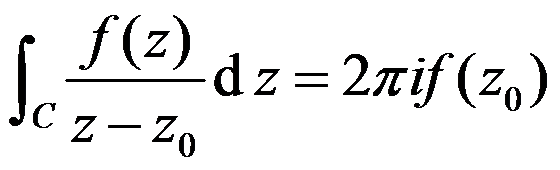 。( )
。( )
选项:
A:对
B:错
答案: 【】
4、判断题:
设C为正向圆周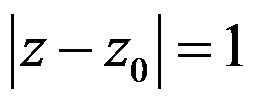 ,
, 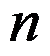 为整数,则积分
为整数,则积分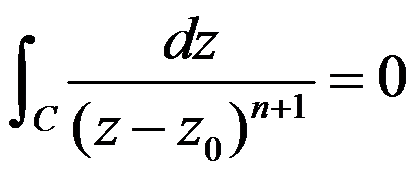 必成立。( )
必成立。( )
选项:
A:错
B:对
答案: 【】
5、判断题:
设 在
在 内解析,则
内解析,则 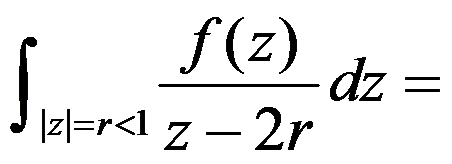 0。( )
0。( )
选项:
A:错
B:对
答案: 【】
第四章 单元测试
1、单选题:
设幂级数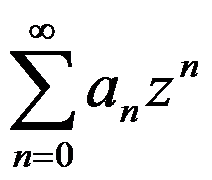 的收敛半径
的收敛半径 ,则它( )。
,则它( )。
选项:
A:在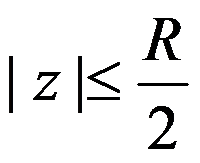 上一致收敛
上一致收敛
B:在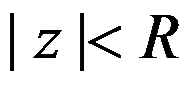 上一致收敛
上一致收敛
C:在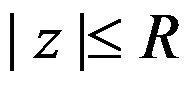 上收敛
上收敛
D:在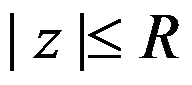 上绝对收敛
上绝对收敛
答案: 【
2、单选题:
可以使f(z)=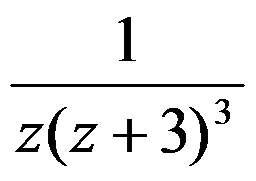 在点z=0处的罗朗展开式收敛的区域是( )。
在点z=0处的罗朗展开式收敛的区域是( )。
选项:
A:0<|z-2|<2
B:0<|z|<+∞
C:0<|z-2|<+∞
D:0<|z|<2
答案: 【】
3、判断题:
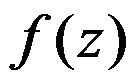 在
在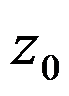 处可展成泰勒级数与
处可展成泰勒级数与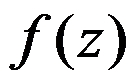 在
在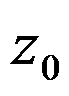 处解析等价。( )
处解析等价。( )
选项:
A:对
B:错
答案: 【】
4、判断题:
若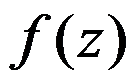 在
在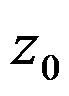 处解析,则它在该点的某个邻域内可展开为幂级数。( )
处解析,则它在该点的某个邻域内可展开为幂级数。( )
选项:
A:对
B:错
答案: 【】
5、单选题:
幂级数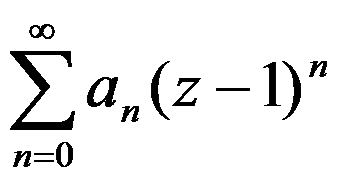 在点
在点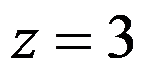 收敛而在
收敛而在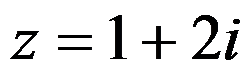 发散,则它的收敛半径是( )。
发散,则它的收敛半径是( )。
选项:
A:0
B:2
C:1
D:-2
答案: 【】
第五章 单元测试
1、单选题:
已知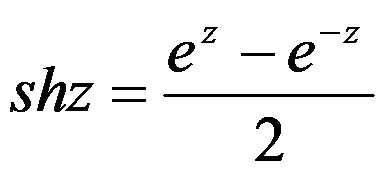 及
及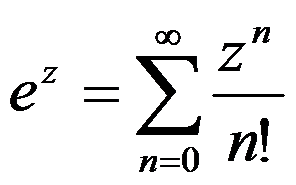 ,则
,则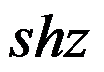 的幂级数展开式为( )。
的幂级数展开式为( )。
选项:
A: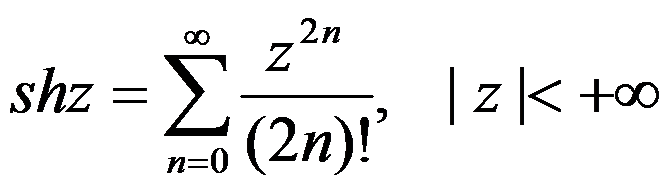
B: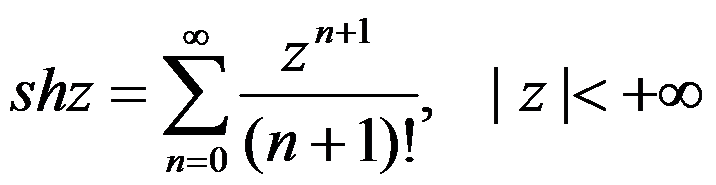
C: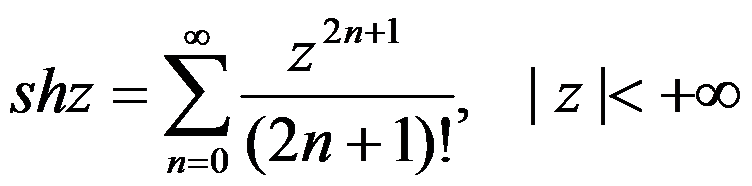
D: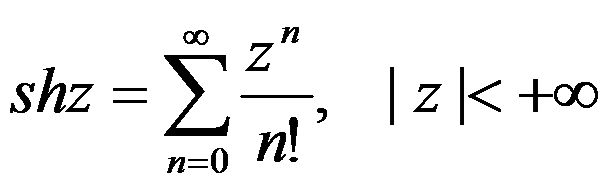
答案: 【
】
2、单选题:
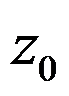 为
为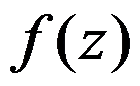 的
的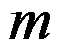 阶零点是
阶零点是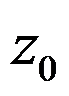 为
为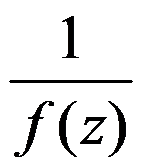 的
的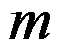 阶极点的( )。
阶极点的( )。
选项:
A:充要条件
B:充分条件
C:必要条件
D:这三项都不对
答案: 【】
3、判断题:
设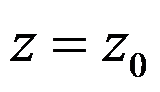 是函数
是函数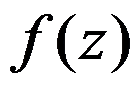 的本性奇点,则
的本性奇点,则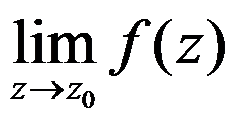 不存在也不为
不存在也不为 。( )
。( )
选项:
A:对
B:错
答案: 【】
4、判断题:
设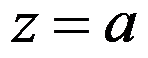 是
是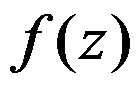 的
的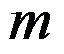 阶极点,则
阶极点,则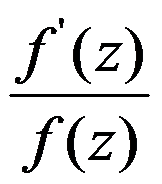 在
在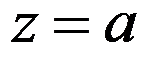 处的留数为m。 ( )
处的留数为m。 ( )
选项:
A:错
B:对
答案: 【】
5、判断题:
设函数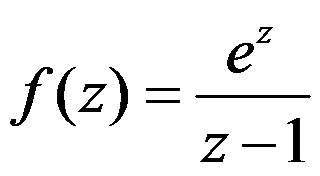 ,则
,则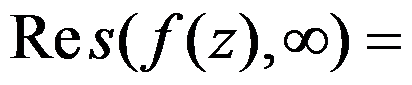 -e。( )
-e。( )
选项:
A:对
B:错
答案: 【】
第六章 单元测试
1、单选题:
映射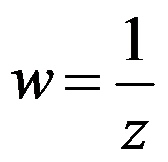 在点
在点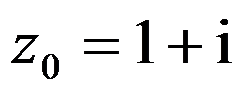 处的伸缩率和旋转角分别为( )。
处的伸缩率和旋转角分别为( )。
选项:
A: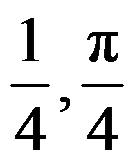
B: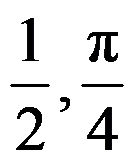
C: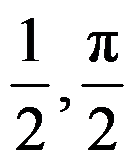
D: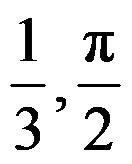
答案: 【
】
2、单选题:
把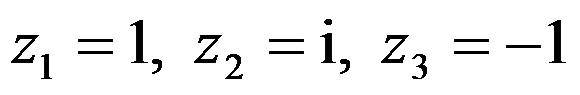 分别映照为
分别映照为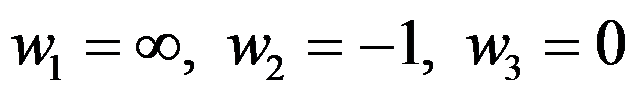 的分式线性函数答案为( )。
的分式线性函数答案为( )。
选项:
A: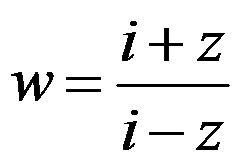
B: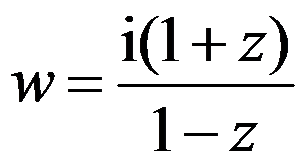
C: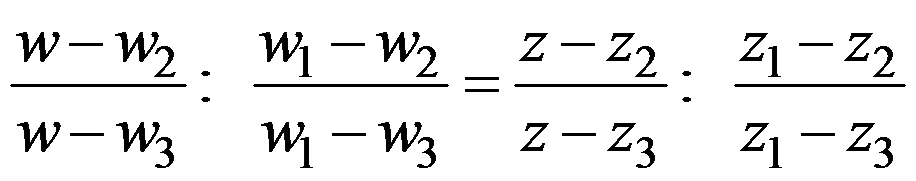
D: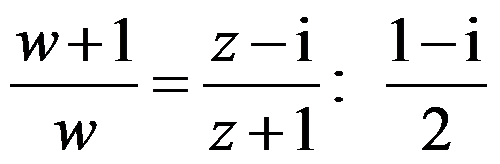
答案: 【
】
3、单选题:
将上半平面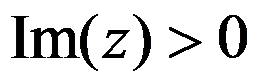 映照成单位圆
映照成单位圆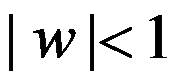 内的分式线性函数的一般形式为( ) 。
内的分式线性函数的一般形式为( ) 。
选项:
A: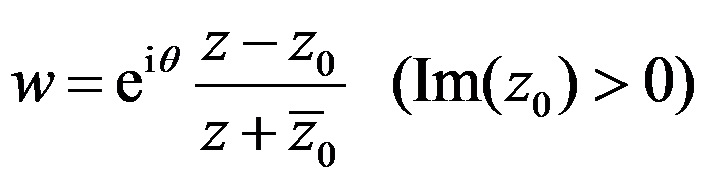
B: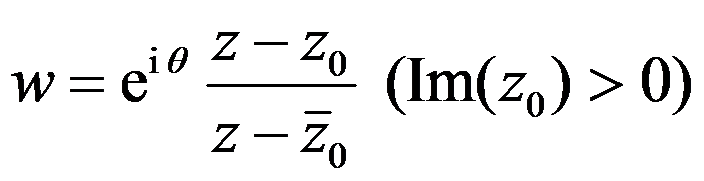
C: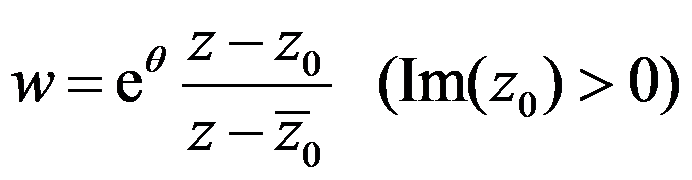
D: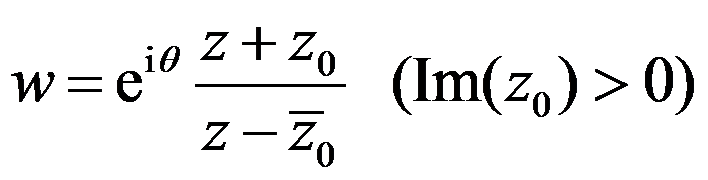
答案: 【
】
4、判断题:
解析函数的导数的几何意义是伸缩比和转动角。( )
选项:
A:对
B:错
答案: 【】
5、判断题:
若分式线性映照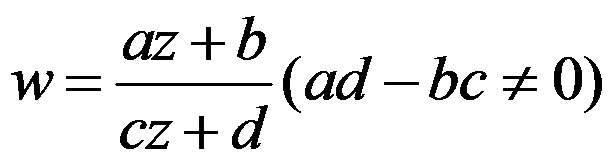 将
将 平面上圆周
平面上圆周 的内部,那映照为
的内部,那映照为 平面上的圆周
平面上的圆周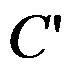 的外部.那么,
的外部.那么, 的外部整个映成
的外部整个映成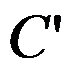 的内部。( )
的内部。( )
选项:
A:错
B:对
答案: 【

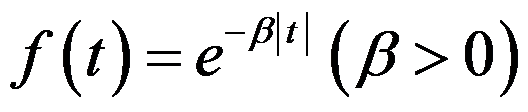 则
则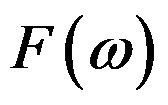 =( )。
=( )。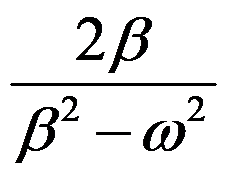
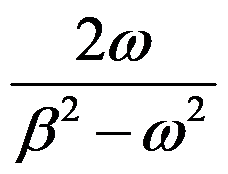
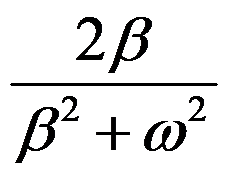
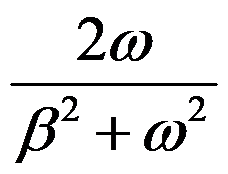
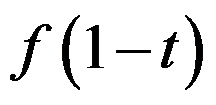 的傅里叶积分为( )。
的傅里叶积分为( )。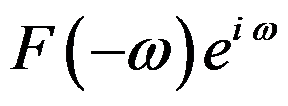
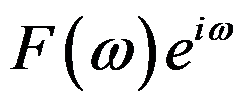
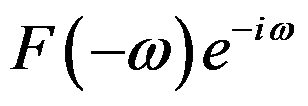
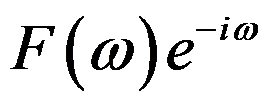
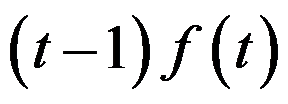 的傅里叶积分是( )。
的傅里叶积分是( )。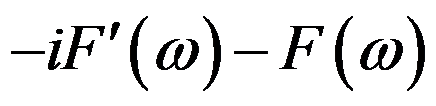
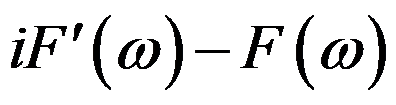
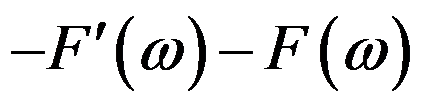
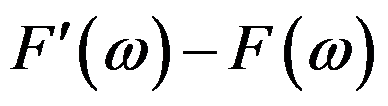
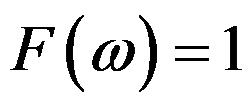 ,则
,则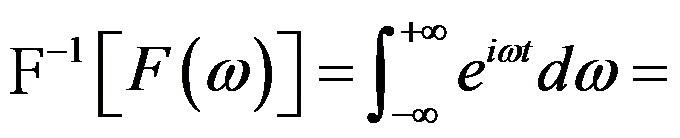 0。( )
0。( )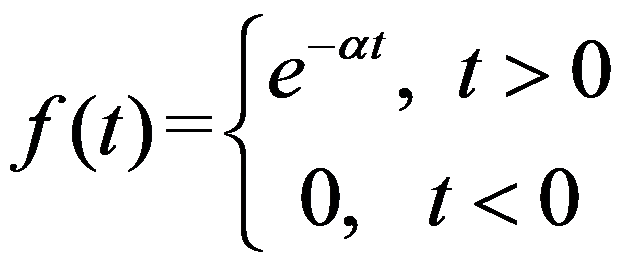 (其中
(其中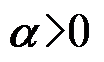 )的傅里叶变换是
)的傅里叶变换是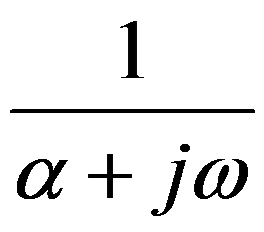 。( )
。( ) 为定义在
为定义在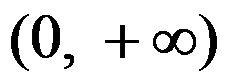 上的实值(或复值)函数,其拉普拉斯积分收敛,建立
上的实值(或复值)函数,其拉普拉斯积分收敛,建立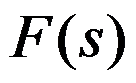 之间对应的拉普拉斯变换(简称拉氏变换)
之间对应的拉普拉斯变换(简称拉氏变换)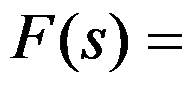
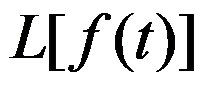 的积分是( )。
的积分是( )。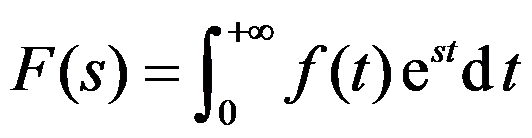
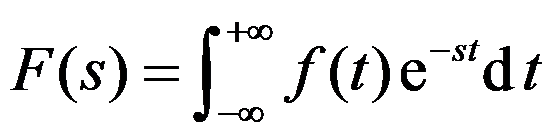
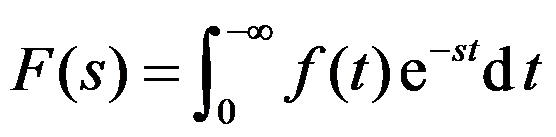
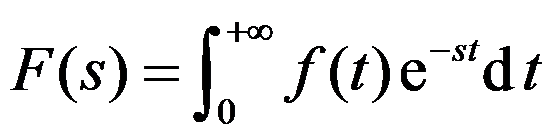
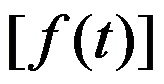 ,则建立
,则建立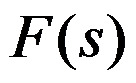 与
与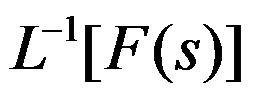 的积分是( )。
的积分是( )。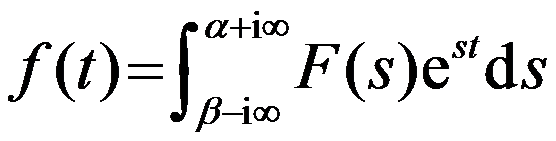
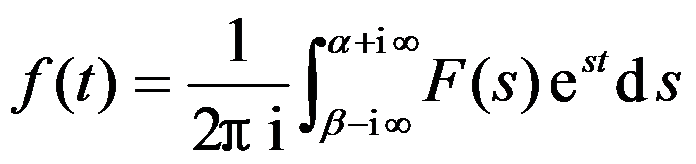
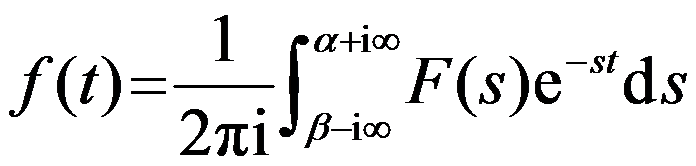
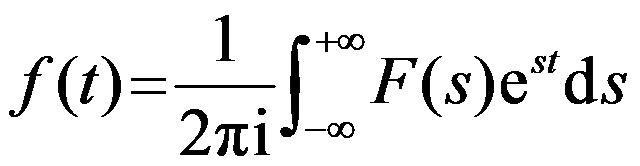
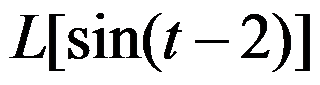 的值为( )。
的值为( )。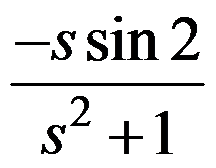
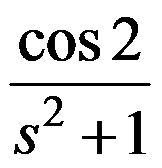
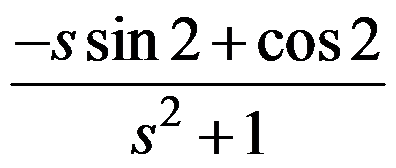
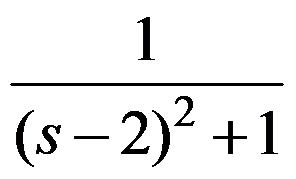
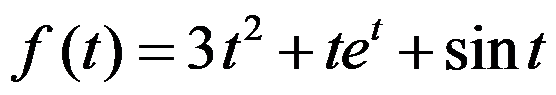 ,则函数
,则函数 的拉普拉斯变换为
的拉普拉斯变换为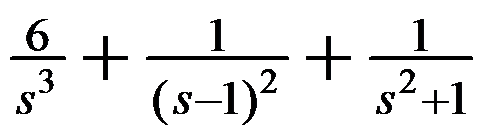 。( )
。( )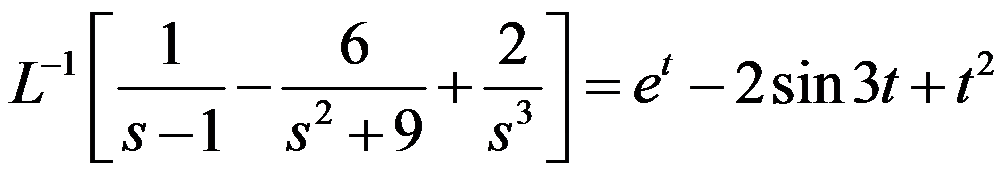 。( )
。( )
评论0